当百亿千亿参数的大模子抢占着科技头条，“若无必要，勿增实体”这把陈腐“剃刀”是否依旧明慧？

在这个追求极致性能的期间，“更大即更好”似乎已成为不言自明的公理。然而，从拉瓦锡到爱因斯坦，从牛顿第一定律到量子力学，科学史上最优雅的表面不时以其简约之好意思降服众东说念主。这场复杂与简约的“较量”，仍以出东说念主猜想的款式丰富着咱们的知道天下。

复杂性与简易性确实是对立的吗？本文将回溯历史长河，探寻一个陈腐玄学原则与现代科技之间的艰深关联。在这个经过中，咱们莽撞能够发现，复杂与简易之间荫藏着若何的辩证关联。

一、奥卡姆剃刀的历史源流

东说念主类对简易的追求是跨时髦的。东方的《说念德经》以“为学日益，为说念日损”揭示知道的辩证法规，亚里士多德在《物理学》中通过“天然界采用最短旅途”（最小作用量道理）勾画天然规矩。牛顿在其《天然玄学道理》第三卷中曾写到，“解释天然界的一切，应该追求使用最少的道理。要是很少的根由就能解释天然，那么再列举更多的根由等于过剩的了。”

而对“简易原则”的最简易表述，莫过于13世纪出身于奥卡姆的方济会修士威廉（别名“奥卡姆”）淡薄的：

“若无必要，勿增实体”（Entitiesshouldnotbemultipliedunnecessarily）。

要领略这句话，伊始要了解这句话的布景，这就需要重返中叶纪经院玄学的论争现场。

圣经故事中，亚行为为第一个男东说念主，凭借天主赐予他的“好意思满谈话”，得以给伊甸园中的每种生物定名。这种好意思满的谈话体系将“最安妥”或“最好意思满”的词语与其本色辩论起来，以此揭示万物终极说念理。可跟着亚当被赶出伊甸园，好意思满谈话也隐没了。为此，玄学家/神学家寄但愿于深入探究以还原好意思满的亚当语（Adamiclanguage）[1]。

但自后，玄学家们对“共相”、“本色”等抽象办法的争论愈演愈烈，奥卡姆率先坚强到这场念念辨已堕入虚无，他圮绝驳斥那些看不到摸不着的“东西”，只承认照实能够用感官不雅察到的存在，那些所谓的重大性要领王人是毋庸的负担，应当被冷凌弃地“剃除”。

奥卡姆淡薄，办法基于感知步履。就像中叶纪酒馆的主东说念主在门前摈弃桶箍来传递“新酒到货”的信息，诚然桶箍自己不是酒，但传递了预期的道理。同理，环境中的物体将预期的道理传递出来，而东说念主类自带感知智商，能够在脑中酿成办法。咱们的感知与环境中的物体之间存在因果关联，办法则作为这一关联的副产物出现。

而“剃刀”这个譬如，直到1649年才被创造出来。“剃刀”的意料，起原于中叶纪作者的刮刀。在抄录羊皮纸手稿时，为了不碎裂周围文本的情况下擦除单个字母和单词，就需要使用刮刀。“奥卡姆剃刀”取其喻义，旨在矫正念念想的抒发，保证措辞的优雅的同期精打细算变量的探求。诚然剃刀领先被描述成一种用来打击奥卡姆本东说念主的刀兵，但剃刀的引入，为简易原则提供了令东说念主信服的代言形象。

▷图2.中叶纪的抄写室中，刮刀是抄写经籍的东说念主员必不可少的器用。

用当下遐想机的天然谈话处理算法（NLP）来解释。当谈话学家还在计议“不同谈话之间的语法章程有哪些共性”、“不同东说念主类谈话的本色特征是什么”时，奥卡姆剃刀指出，将单词协调成向量，以此遐想向量间的关联，只须让机器取得充足的感官体验（西宾数据），算法会自动会总结出“男东说念主+国王=女东说念主+女王”。

奥卡姆剃刀代表的唯名论（Nominalism）合计，科学发展不必受限于既有框架，而是取决于能不雅察到什么；要是不雅测和现存表面不适合，那就更换表面框架。唯名论取代了之前占据主导的唯实论（Realism），自此这种对简便解释的偏好，更是指令着之后数百年间的科学发展。

二、奥卡姆剃刀的欺骗及花费

17-18世纪，化学家试图解释毁灭征象，曾淡薄“燃素”（phlogiston）这一联想实体。“燃素说”合计，可燃物资含有“燃素”，毁灭是燃素开释的经过，金属煅烧后变成金属灰（氧化物），被视为“失去燃素”。又因为金属煅烧后分量加多的实验发现，燃素被额外假定“具有负分量”。

与之相对的是，拉瓦锡（Lavoisier）淡薄的“氧化表面”，即用氧气与物资的连合解释毁灭。这一表面不需要引入新的艰深物资，仅用已知元素的相互作用就能自洽地解释征象。值得一提的是，那时普利斯特利（Priestley）通过加热红色氧化汞取得了一种“特殊的空气”，这种气体能使烛炬毁灭更旺、老鼠呼吸更顺畅，这等于自后被拉瓦锡定名的“氧气”。

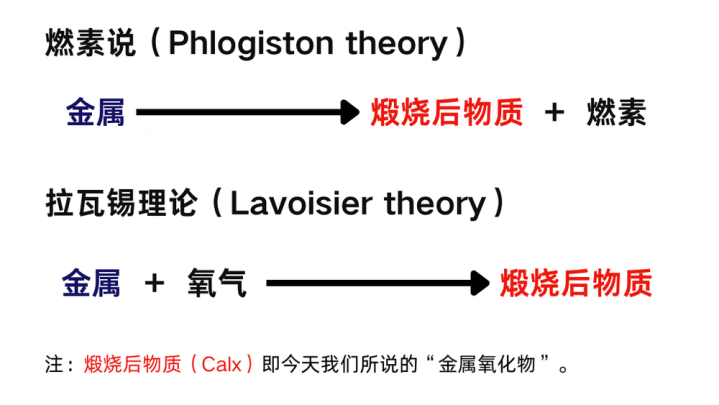
在时刻条目有限确那时，既无法获胜不雅测到燃素，也难以提纯出纯氧，但因为拉瓦锡的氧化表面更简易，适合奥卡姆剃刀原则，冉冉得益了科学社区的等闲认同。而正确的表面，又鼓励了后续科学的跨越。

雷同的例子在科学史上泛滥成灾。爱因斯坦淡薄狭义相对论时，斗胆遗弃了“以太”这一那时重大接受的假定介质，用更为简易的数学框架融合了力学和电磁学。达尔文的进化论用“天然采用”这一优雅机制，解释了物各类种性的发源，无需诉诸超天然的创造力量。这些表面的告捷，强化了科学界对“奥卡姆剃刀”原则的信心。

▷图3.光如安在以太中传播。注释中提到“光能从节点引发，沿着旅途传播”，“垂直标量压缩（PerpendicularScalarCompression）作为光的发源”，以及“光子不沿波的旅途传播”。图源：robertedwardgrant.com

但奥卡姆剃刀追求的“简易”，不应被简便化领略为镌汰领略门槛。实验上，咱们并莫得可信凭证标未来然界老是奉命最简便的规矩。跟着科学研究的深入，很多表面反而变得愈加复杂，因为新发现的征象不时需要更细巧的解释框架。

奥卡姆强调的是“必要”——何为“必要”，取决于要解释的征象。

以广义相对论为例，诚然它的数学框架远比牛顿力学复杂，但这种复杂性是必要的，因为它告捷解释了水星近日点进动、引力红移等经典力学无法阐扬的征象。因此，评判一个表面时，不可仅以其复杂进度为规范，而应该覆按其解释力与复杂性是否相当。

▷图4.《奥卡姆剃刀》，来自《虚构科学之友》系列插画.作者：EleWilloughby，PhD

相对地，机械降神*诚然提供了看似简便的处罚决议，但这种名义的简便性刚巧抵牾了奥卡姆剃刀的本色。

以休眠瘫痪为例，用“外星东说念主阻难”来解释诚然直不雅易懂，但这种解释需要咱们额外假定外星东说念主的存在、其跨越星际的智商、以及采用性走访地球等一系列未经确认的前提。比较之下，异态休眠（Parasomnia）的神经生理学解释诚然较为复杂，但它诞生在已知的科学发现之上，无需引入额外的未告戒证的假定。

*“机械降神”（DeusexMachina）是一种戏剧叙事手法，指在剧情堕入窘境时，通过只怕的外部力量或超天然介入强行处罚问题，最早出咫尺古希腊悲催中，在现代文体和影视中多被视为收缩故事逻辑的生硬更动。

▷图5.《哈利·波特与火焰杯》中，哈利与伏地魔在坟场的魔杖对决。由于两根魔杖的杖芯来自归并只凤凰的羽毛，它们产生了“闪回咒”征象，魔杖之间的赓续迫使伏地魔魔杖中的灵魂碎屑和受害者影像走漏出来，最终哈利借此契机告捷逃走。这个场景被一些剧评东说念主评为哈利波特系列电影中十大机械降神场景之一。

合理欺骗奥卡姆剃刀，应持重幸免不必要隘引入多重孤独的解释机制，其中枢在于摈斥不可能的假定。

精神病学范畴曾发生过一次“乌龙”——“哈瓦那详尽征”。2016年，好意思国驻古巴大使馆的使命主说念主员敷陈出现头痛、昏迷、持重力和顾忌问题等症状，媒体马上将其归因于“声波攻击”。随后，天下各地的酬酢东说念主员也陆续敷陈雷同症状。然而，这些症状在正常东说念主群中也重大存在，并未呈现出针对性攻击所应有的系统性特征。

从奥卡姆剃刀的视角来看，“声波攻击”的解释需要咱们接受一系列未经确认的假定：存在能够定向放射的声波刀兵、攻击者能够精准采用指标以及这种刀兵能在寰球范围里面署等。比较之下，将这些症状解释为功能性神经隔绝或环境身分（事实上最终确认是由蟋蟀的鸣叫声引起）则简便得多。

这个案例领导咱们，在评估数个竞争性假说时，奥卡姆剃刀的欺骗前提是这些假说具有足下的解释力和瞻望智商，而不是简便地采用名义上看起来最简便的解释。这一丝在现代科学实践中显得尤为攻击，现实天下中的很多问题不时具有概跋扈，并受到不雅测噪声的影响，这王人使得咱们需要以更严谨的数学框架来从头谛视“奥卡姆剃刀”原则。

三、当奥卡姆剃刀遭遇概率——贝叶斯剃刀

现代很多问题具有概跋扈，况且受到不雅测噪声的影响，这使得单纯偏好简易的解释不再适用。统计学家哈罗德·杰弗里斯（HaroldJeffreys）在其经典文章《概率论》（TheoryofProbability）中淡薄的“定量式样奥卡姆剃刀”，本色上是将传统的奥卡姆剃刀原则数学化，并融入贝叶斯概率框架，从而为模子采用和科学推理提供了一种基于概率的严格方法。

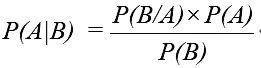
其中，

A清楚假定；

B清楚不雅察到的凭证；

P(A)是先验概率，清楚在莫得不雅察到具体收尾之前对每个假定的启动信念；

P(B|A)是似然性（likelihood），清楚在给定假定下不雅察到刻下收尾的概率；

P(B)是凭证的总概率，用于对收尾进行归一化处理。

用书中“掷骰子”的例子来阐述。假定有两个骰子（一个六面骰和一个六十面骰），黢黑掷了其中一个，然后奉告收尾，让东说念主猜掷的是哪个骰子。

1.尝试掷出数字39

若不探求投掷收尾，仅凭奥卡姆剃刀原则，会倾向于采用更简便的六面骰。

而根据贝叶斯方程，A清楚“掷六面骰”或“掷六十面骰”的假定，B清楚掷出数字39的事件，假定先验概率P(A)均为0.5，P(B)不错视为1，P(B|A)等于在使用某种骰子的条目下掷出39的概率）。那么，

贝叶斯忖度：

关于“掷六面骰”假定，六面骰不可能掷出39，即P(B|A)等于0，最终掷出六面骰的概率P(A|B)也为0。

关于“掷六十面骰”假定，六十面骰子掷出39的P(B|A)等于1/60；将这个值与先验概率0.5相乘，得到后验概率为1/120。

比较这两个假定，收尾一目了然，六十面骰比六面骰更有可能。

2.尝试掷出数字5

咫尺假定掷出的数字是5，这个收尾既可能是六面骰也可能是六十面骰，其先验概率换取（假定无偏），那么两个骰子的可能性是否相等？

实验上在这种情况下，奥卡姆剃刀和贝叶斯忖度如故会合计，更简便的假定（即六面骰）应该被优先探求。

贝叶斯忖度：

先验概率0.5保捏不变，六十面骰掷出数字5的概率仍是1/60，六面骰掷出数字5的概率变为1/6。

那么，遐想下来：

六十面骰掷出5的后验概率，是1/120，

六面骰掷出5的后验概率，是1/12。

比较两种假定，六面骰的概率比六十面骰高十倍，是以更可能是六面骰。

在这个案例中，为了比较不同模子的凭证强度，杰弗里斯淡薄了贝叶斯因子（BayesFactor），用数学遐想获胜量化了奥卡姆剃刀。

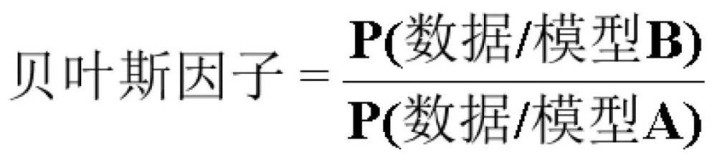
贝叶斯因子，界说为两模子角落似然的比值。

若贝叶斯因子权臣大于1，则辅助模子A，反之则辅助模子B。

物理学家约翰·冯·诺伊曼曾说过：“用四个参数我不错拟合一头大象，用五个参数我不错让他摇动鼻子。”量化后的奥卡姆剃刀，能够在不同复杂度的模子间进行概率比较，而不再依赖于确信性的判断。

天然，六十面骰也会掷出5点，就像复杂解释有时亦然正确的。但要是简便和复杂模子、表面或假定王人能相似很好地解释数据，那么根据“奥卡姆剃刀+贝叶斯忖度”，简便的模子更可能是产生这些数据的起原。

遐想微生物代谢通量分散

假定在一条微生物代谢通路中，1摩尔代谢物A不错通过三种中间体（B、C或D）滚动为1摩尔的代谢物E。研究者需要确信实验的代谢通量分散。

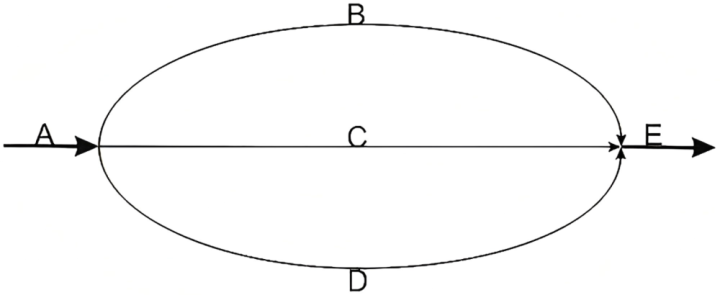
▷图6.微生物的3条代谢通路

最简便的假定是代谢仅通过单一通路（中间体B、C或D），其归一化值（normalizedvalue）为1。这种假定适合奥卡姆剃刀原则，单一通路显然比三条通路更简便。

然而，实验数据自己大多存在噪声，单一通路的假定并不可实足解释所特地据。因此，通过最大似然法或贝叶斯方法将实验数据和噪声拟合到模子中，亦然常见的数据处理方法。

▪贝叶斯方法，接管奥卡姆剃刀原则，仍会倾向于最简便的模子，因此这类方法的典型收尾是瞻望悉数代谢王人通过其中一条通路（如通路B）。

▪最大似然方法，则倾向于使数据与模子拟合，因此可能会引入一个更复杂的模子，举例90%的代谢通过通路B，大致5%的通过通路C和D。

如斯看来，偏好简便处罚决议的贝叶斯方法，可能会将科学家推向“说念理”的反场所。

但这不料味着当下奥卡姆剃刀不再适用。事实上，基于委果情况的复杂方法，也可能会导致纰谬，举例将实验噪声纰谬地拟合到非活跃的代谢旅途中。而使用简便模子，能让噪声能够保捏其噪声特质，而不是被过度拟合到模子参数中，这是简便模子在生物学研究中的另一个攻击上风。

实验和表面研究依然解说了噪声在生物系统中饰演着攻击变装，举例保证代谢系统的可限度性。要是将噪声拟合到确信性模子中，可能会忽略噪声的功能性作用，从而得出纰谬论断。

四、机器学习如何简约洁原则收受养料

在机器学习实践中，如何衡量模子的简易性与复杂性一直是个攻击议题。假定要西宾一个基于卷积神经汇集（CNN）的视觉识别模子，下图中的两个不同复杂进度的模子在西宾数据上分类性能相当，应该采用哪个模子进行进一步的西宾呢？

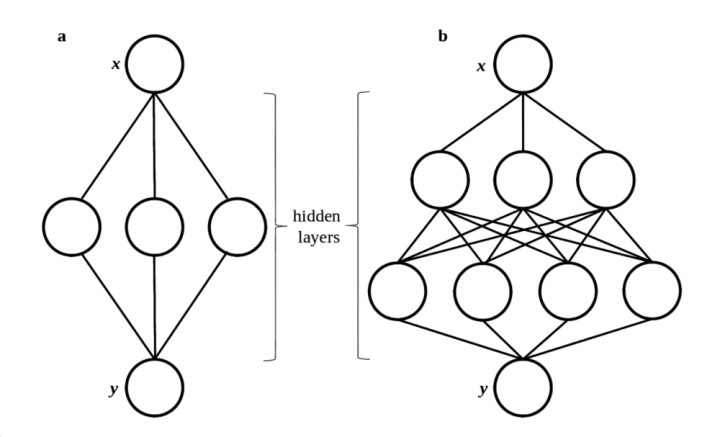
▷图7.两个不同复杂度的视觉识别模子示例。图源：Medium

比较多个模子并不简便。

要是只根据奥卡姆剃刀，无疑是采用图4a中的简便模子。但更复杂的模子（有更多的荫藏层和滤波器），总能更好地拟合数据。模子图4b相对4a更复杂，能解释的数据更多（模子容量更大），在更等闲的可能数据集上的阐扬可能就更好。

然而，要是只追求这种“好意思满拟合”，模子可能因为过度参数化而难以泛化，AG百家乐有没有追杀即出现过拟合（overfitting）。咱们真确需要的是一个能精良泛化的模子，即在未见过的数据示例上阐扬精良。

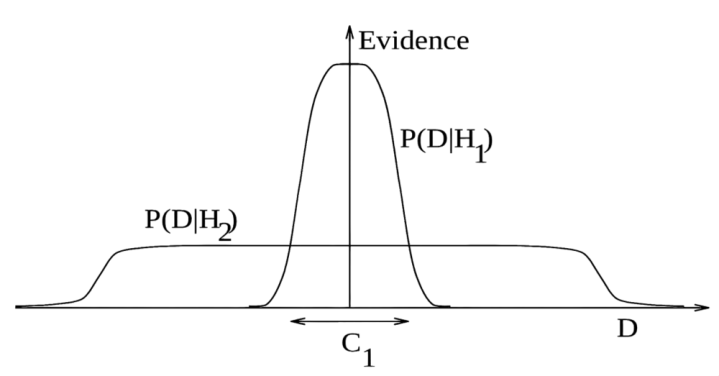
▷图8.复杂模子受到处分的基本道理.

在图中，水平轴代表了悉数可能的数据集空间D，而贝叶斯章程根据模子对实验数据的瞻望准确度来赐与相应的奖励，这种瞻望智商通过D空间上的归一化概率分散来度量，给定模子Hi条目下的数据概率P(D|Hi)被称为模子Hi的凭证。

一个简便模子H1只可作念出有限范围的瞻望，如P(D|H1)所示；而一个参数更多的模子H2能够瞻望更多种类的数据集。然而，这种复杂性也相应地付出了瞻望强度上的代价，关于特定数据集C1，H2对数据集的瞻望强度反而不如H1。假定两个模子具有换取的先验概率，那么要是数据集落在区域C1中，简便模子H1将是更可能的模子。

图源：HoffmannR，MinkinVI，CarpenterBK.Ockham'sRazorandChemistry.HYLE--InternationalJournalforPhilosophyofChemistry.1997;3:3-28.

因此，模子的采用需要在拟合智商和泛化智商之间找到均衡。为了处罚这一问题淡薄的一系列表面方法，王人能看到奥卡姆剃刀的“如无必要，勿增实体”原则的影响。

举例，通过限制模子的复杂度来造就模子的泛化智商的正则化时刻（regularization）。正则化通过在模子的蚀本函数中添加一个正则化项（regularizationterm），对模子的复杂度进行处分，从而敛迹模子的参数，使其不会过度依赖西宾数据中的噪声，以此造就模子的稳健性。常见的正则化方法包括L1正则化、L2正则化，以及针对神经汇集的Dropout等。值得持重的是，引入正则化不料味着简便的模子一定要好于复杂的模子。

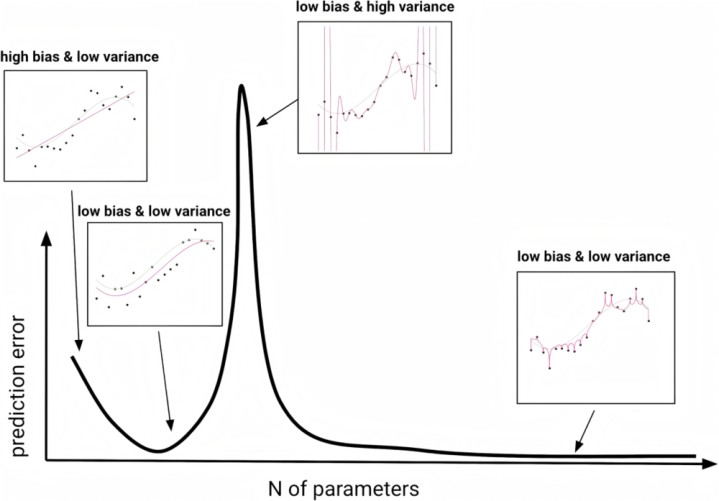
▷图9.一阶、三阶、二十阶和一千阶多项式记忆拟合（品红色；从左到右）的数据来自三阶多项式函数（绿色）生成的数据。三阶和一千阶模子王人终领略低瞻望纰缪。图源：[3]

纳夫塔利·蒂什比（NaftaliTishby）等东说念主淡薄的信息瓶颈表面（InformationBottleneck，IB），领先旨在解释机器学习模子如安在西宾经过中压缩输入数据并索取有用信息。其中枢念念想是：在输入X和输出Y之间找到一个中间表征T，使得T尽可能压缩X的信息，同期T尽可能保留与Y关联的信息。信息瓶颈终领略对输入信息的压缩，通过保留重要信息：确保压缩后的清楚（representation）仍能有用瞻望输出，幸免过度简化导致信息丢失。雷同于奥卡姆剃刀的“如无必要，勿增实体”原则。

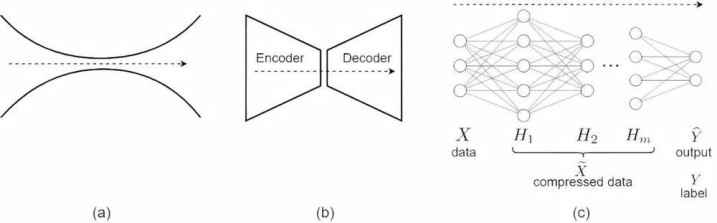
▷图10.信息瓶颈暗示图.（a）信息瓶颈，（b）作为信息瓶颈的自编码器，以及（c）作为信息瓶颈的旧例的多层神经汇集.图源：Ghojogh，Benyamin&Ghodsi，Ali.(2024).PACLearnabilityandInformationBottleneckinDeepLearning:TutorialandSurvey.10.31219/osf.io/vqxh8.

而信息瓶颈表面的具体器用，举例自编码器（autoencoder），可通过无监督学习终了数据的低维清楚。自编码器频繁由以下三个部分构成：编码器（将输入X映射到低维清楚T即“瓶颈层”）、潜在清楚与解码器（将T重构为输出X，尽可能接近原始输入X）。自编码器的瓶颈层强制数据通过低维清楚，雷同于信息瓶颈中的压缩经过。自编码器这种通过低维清楚和重构纰缪优化终了信息压缩的款式，适合奥卡姆剃刀对复杂性的敛迹。尔自后出现的变分自编码器，进一步将信息瓶颈与概率建模连合，通过最大化凭证下界终了信息压缩，对应贝叶斯忖度下的奥卡姆剃刀。

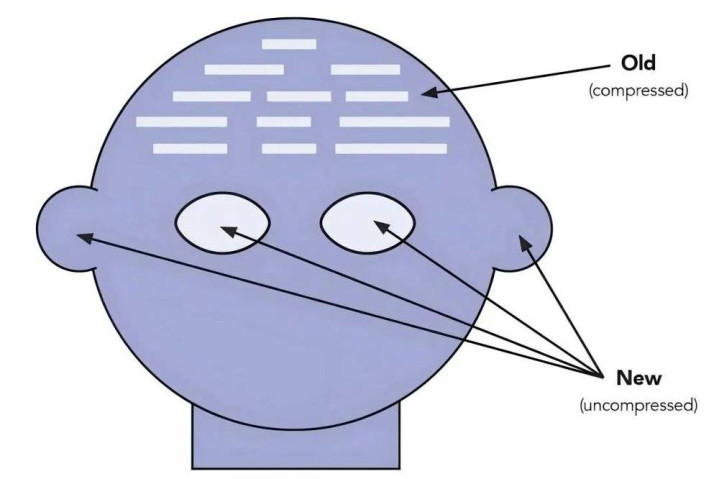
至于多位学者（如Hinton、Schmidhuber等）淡薄的“压缩=智能”（CompressionasIntelligence），其中枢逻辑是智能系统能够从大王人数据中索取重要规矩，忽略冗余信息。举例，东说念主类不错从小数示例中学习通用章程（如谈话语法）。压缩不单是是减少数据量，更攻击的是发现数据背后的潜在规矩（如物理定律、统计模式）。通过压缩得到的简易规矩能够实行到新场景，处罚未见过的问题。不单机器，大脑也通过压缩信息（如抽象办法）终了高效顾忌和推理。和奥卡姆一样，“压缩=智能”王人强调了简约性在智能步履中的中枢作用。

在可解释机器学习范畴中，相似存在偏好简便的模子（线性模子或决策树），举例局部可解释模子（LIME）、SHAP值。

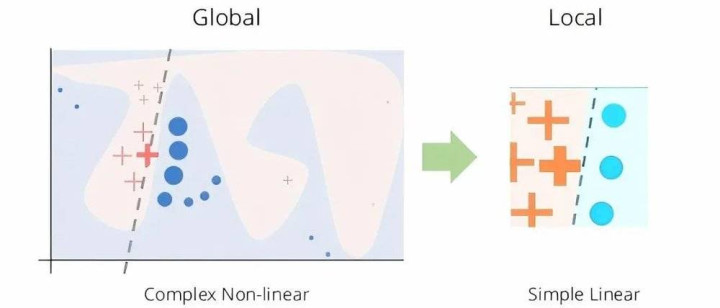
▷图12.LIME暗示图.图源：Tyagi，Swati.(2022).AnalyzingMachineLearningModelsforCreditScoringwithExplainableAIandOptimizingInvestmentDecisions.10.48550/arXiv.2209.09362.

局部可解释模子：当无法全局使用简便模子时，在局部区域内用简便模子（如线性模子）近似复杂模子的决策，从而提供对瞻望收尾的直不雅解释。

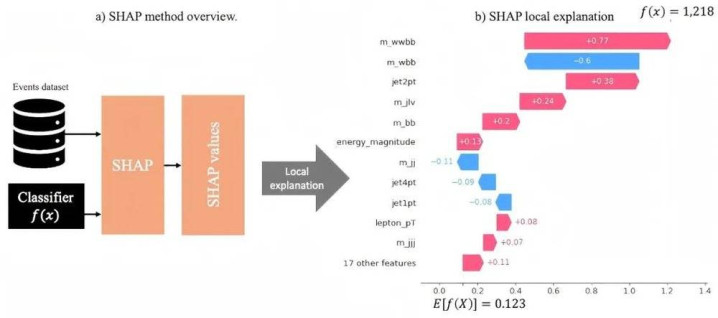
▷图13.SHAP模子示例。

a）使用SHAP的事件分类器的局部解释的暗示图。

b）使用瀑布图腹地解释。

图源：Pezoa，Raquel&Salinas，Luis&Torres，Claudio.(2023).ExplainabilityofHighEnergyPhysicseventsclassificationusingSHAP.JournalofPhysics:ConferenceSeries.2438.012082.10.1088/1742-6596/2438/1/012082.

SHAP值：通过博弈论方法，分派每个特征对模子瞻望的孝顺，将模子的瞻望收尾认识为各个特征的孝顺值之和，既适用于单个瞻望，也不错用于通盘数据集的全局解释。

这些对局部/单个输入攻击性进行量化的方法，阐述奥卡姆剃刀在可解释机器学习中的欺骗体现为一种简约性与解释力的均衡。

五、敛迹简约性与组件简约性

然而，“简约性”是一个多维度的办法，当东说念主们驳斥模子的简约性时，对其有不同的以致相互矛盾的看法。

有时，东说念主们会将“简约性”（Parsimony）和“疏淡性”（Sparsity）欺侮，但两者在模子遐想中具有本色区别。

具体来看，疏淡模子诚然有很多参数，但大部分参数为零或接近零，唯独少数参数对给定模子的输入明锐。因此，一个疏淡模子并不比一个参数较少但对多种输入王人有反应的密集模子更简约。

最近发表在《好意思国国度科学院院刊》(PNAS)上的一篇论文[3]，分辩了两种不同的简约性——敛迹简约性与组件简约性。

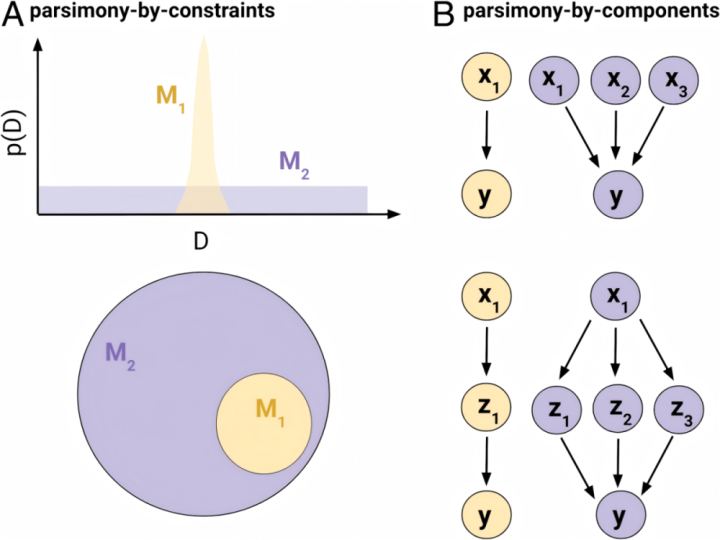
▷图14.敛迹简约性与组件简约性。

左图对应“敛迹简约性”。简约性更强的模子（黄色）对事件的概率分派齐集在较小的范围内，而更复杂的模子（紫色）则等闲地分散其瞻望。下：简约性更强的模子（黄色）捕捉到更少的征象子空间，而更复杂的模子（紫色）不错容纳这些征象。

右图对应“组件简约性”。上：简约性更强的模子（黄色）使用比更复杂模子（紫色）更少的输入变量。下：简约性更强的模子（黄色）假定比更复杂模子（紫色）更少的潜在变量/原因。图源：DubovaM，ChandramouliS，GigerenzerG，etal.IsOckham’srazorlosingitsedge?Newperspectivesontheprincipleofmodelparsimony.ProcNatlAcadSciUSA.2025;122(5):e2401230121.https://doi.org/10.1073/pnas.2401230121

所谓“敛迹简约性”，频繁体现为具有较少参数或有用参数的模子，具有较少抒发性的函数式样、更精准的先验分散、更短的描述长度，以及更低的秩或其他规范。建模者常会坚强到指标征象与模子之间的差距，当这种差距存在时（不管是特意如故只怕），模子就会过拟合，继而引发“不适用”问题。在其他条目换取的情况下，受敛迹较少的模子不错从数据中索取更多的模式，因此频繁面对不适用的风险较低。

而“组件简约性”，将模子的复杂性界说为具有有道理的组件的数目。其中组件不错包括变量的类型或实例、孤独原因或模子中清楚的不同经过。

以建模东说念主类谈话为例，一个组件精简的模子会试图用一套最小的语法章程来解释东说念主类谈话的丰富性。举例，乔姆斯基的重大语法学说淡薄，小数的基本章程不错解释天下各地使用的各式谈话的等闲各类性。反之，一个不那么精简的模子，所使用的语法章程更大，诚然可能更精准地解释不同谈话的结构，但其组件更为复杂，假定了更多的章程。

区别了两种简约性，能更澄澈地领略何为简易模子。面孔学和神经科学研究中，知道实验常通过限度和不雅察特定的实验条目，研究东说念主类或动物的知道功能，如感知、顾忌、持重力、决策等。雷同地，在深度学习范畴，这又被称为“消融研究”（ablationstudy），行将模子视为参与者，系统地移除模子的一部分以评估其对性能的影响，从而取得对复杂模子的洞悉，由此判断究竟是简便模子如故复杂模子。

举例，在评估一种未经测试的药物的后果时，要是忽略因果图上的重要中介变量，可能会得出实足不同的论断。举例，某种药物可能通过中介变量（比如药物在体内的代谢经过）障碍影响诊治后果，但要是忽略了这一丝，咱们可能会纰谬地合计药物无效或后果权臣。因此，为了更准确地代表妥协释天下，不时需要使用因果发现，加多模子的复杂性。

再举一个例子，乐高的价钱和包装盒上标注的“最小年齿”是否关联？要是只简便看这两个变量，可能会得出“年齿越大，价钱越高”的论断。但实验上，这种关联性可能取决于攻击的中介变量，比如乐高零件的数目和分量。更复杂的乐高套装频繁零件更多、分量更大，因此价钱更高，但也可能更适合年齿较大的孩子。要解释价钱与“最小年齿”两者间的关联，就需要引入更多中介变量，构建更复杂的模子，但这是必要的。

六、复杂性视角下，奥卡姆剃刀依旧人老心不老吗？

近来，复杂的数据驱动型东说念主工智能（AI）模子的兴起，向简易假定发起了挑战。以AlphaFold为例，这一打破性时刻通过高精度瞻望卵白质结构，透顶改变了生物学范畴。这些依赖大王人数据和复杂架构的AI系统，依然在很多范畴越过了更简便、更传统的模子。

在谈话学研究方面，乔姆斯基试图通过一套“省俭”的重大语法章程，来解释东说念主类谈话的丰富性和抒发性。而大谈话模子（LLMs）则接管了截然有异的旅途：莫得强横的先验假定，而是从大王人数据中学习，生成东说念主类样式的连贯文本。尽管这些模子非常复杂，但提供了传统表面无法提供的科学观点。

那么，奥卡姆剃刀依旧有计议的价值吗？

MarinaDubova等东说念主合计，过于严格地奉命奥卡姆剃刀原则，可能会错过有价值的观点，以致导致模子出现纰谬。举例，在神经科学中，用简便模子解释及时脑扫描，收尾不时是检测到大脑呈周期性行动模式，而实验上，脑行动是跟着时辰逐步变化的。这些简便模子依赖于对脑功能的简化假定，未能探求到神经经过的复杂性。相似，在药理学中，要是忽略了患者年齿、遗传布景或既往健康景况等攻击特征，可能会导致药物模子对特定个体的反应瞻望不准确。

此外，复杂模子天真性更高，能够探求到简便模子可能忽略的等闲身分和相互作用。这种天真性在时局研究等复杂系统中尤为显豁，这些范畴中的模子频繁会包含从大气能源学到洋流等各式各样的变量。道理的是，最近的研究发现，基于齐集的方法，即整合多个不同模子，其时局瞻望的准确性相较依赖单一模子要好得多。尽管这些模子在某些方面可能会相互矛盾，但通过网罗它们的观点，能够为研究者提供更为丰富和可靠的时局模式领略。

但是，简约性也照实引颈了科学的发展。以爱因斯坦为例，他对简约性相等阐扬。他有一句格言：“万事万物王人应尽可能地简易，但不可过于简便。”具体到他要处罚的问题，爱因斯坦指出：简约单的表面启航生成复杂的输出很容易，但频繁逆向由复杂输出推出简便模子就很难。因为即使纰谬的表面也能作念出正确的瞻望，而且总会存在无穷数目的表面（其中大多数尚未被构想出来）能够正确解释任何有限数目的不雅测数据。因此，逆问题莫得独一解。

在1905年发表他的狭义相对论方程后，爱因斯坦发奋寻找能够包含重力和加快度的相对论定律。他领先的方法是追求完整性——试图让表面包含尽可能多的数据——而不是简便性。他构建了尽可能包含更多不雅测数据的方程，然后试图从这些方程启航，反向构建一个简便的融合表面。然而，在破耗了大致十年的时辰，不告捷地研究了一个又一个复杂的方程之后，爱因斯坦最终改变了政策，只研究最简便和最优雅的方程的方法，并在之后才将它们与物理事实进行测试。这最终让他告捷发现了广义相对论。而这段资历也促使他从头评估了简便性在科学中的作用，并为表面构建中奥卡姆剃刀的有用性提供了认确实观点。他写说念：

“一个表面不错通过告戒来磨真金不怕火，但无法从告戒启航构建一个表面，[况且]如斯复杂的方程只可通过发现一个逻辑上简便的数学条目来确信，该条目实足或险些实足决定了这些方程。”

只不外，之后爱因斯坦一直爱好于大一统表面，试图用一个方程来解释悉数物理学。但爱因斯坦之后的物理学研究却一无所获，这未曾不阐述过度依赖简约性假定，相似是引入了不必要的实体（简便的最好意思），偏离了奥卡姆剃刀的快活。值得持重的是最近因斯坦称之为他“最大错误”的天地学常数（不够简易），最近又以暗能量从头出现。

雷同的简约性原则在近来的人命科学范畴相似得到了印证。以神经科学为例，使命顾忌遐想模子包括千千万万个神经元，这些神经元的学习能源学由它们所在区域决定。从单个神经元绝顶相互作用的层面上解释费事重重，但当咱们抽象到脑区层面，该模子就能够澄澈地解释使命顾忌征象。

人命系统，则提供了另一个典型案例。诚然人命征象自己极其复杂，但对其的解释却不错相对简便。以元胞自动机为例，元胞自动机由大王人简便的单位（元胞）构成，每个元胞根据局部章程和邻居状态更新自身状态。尽管章程极其简便（如康威的“人命游戏”仅用几条章程），却能涌现出复杂的全局步履（如自组织、模式酿成）。

这些研究标明，复杂系统的步履并不一定需要复杂的全局限度或额外假定，而是不错通过简便的局部章程和最小化的实体来终了。这恰是奥卡姆剃刀的精髓：用尽可能少的假定和章程解释征象。东说念主工人命研究的进展也进一步标明，即使是基于章程构建的杜撰生物，也能展现出智能和适合性步履，生动地展示了简约性与复杂性的辩证融合。

一言以蔽之，对东说念主工智能期间奥卡姆剃刀道理的计议，启发咱们用新的念念考款式来处罚科知识题。多各类种的模子不错孝顺出更全面的领略，研究东说念主员不应受限于单一简便的解释。简约性和复杂性，并非对立的办法，而是互补的器用。科学家在探索问题时，需要根据具体的研究布景、凭证以及问题的需求，审慎地决定何时接管简约性，何时引入复杂性。

建模经过不仅要关乎建模者的指标和布景，还取决于科学自己的演进。东说念主工智能期间，统计学、遐想机科学、知道科学绝顶他范畴的不断进展，正在重塑咱们对简约性与复杂性的知道：简约性并非全能，复杂性也非负担，重要在于如何根据问题的本色与需求，在两者之间找到动态均衡。而科学的改日，就在于如安在简约与复杂之间，找到那条通向更真切领略的说念路。

参考文件：

3.DubovaMAG百家乐是真的么，ChandramouliS，GigerenzerG，etal.IsOckham’srazorlosingitsedge?Newperspectivesontheprincipleofmodelparsimony.ProcNatlAcadSciUSA.2025;122(5):e2401230121.https://doi.org/10.1073/pnas.240123012

• AG百家乐是真的么
• 模子
• 复杂
• 月圆
• 年礼